The shell method is a powerful technique used in calculus for determining the volume of solids of revolution. Whether you're a student grappling with the complexities of integration or a seasoned mathematician seeking to refine your skills, understanding the shell method can significantly enhance your analytical repertoire. This method is particularly useful when revolving a region around an axis, allowing for an intuitive grasp of how volumes can be calculated through integration.

In essence, the shell method breaks down the solid into cylindrical shells, making it easier to calculate the volume. By visualizing the shape and applying the appropriate mathematical formulas, you can derive the volume of complex geometrical figures that are often encountered in various fields of science and engineering. This article aims to delve deeper into the shell method, providing a thorough overview of its principles, applications, and practical examples.

As we explore the intricacies of the shell method, we will also address common questions that students and professionals alike may encounter. From the fundamental concepts to advanced applications, our goal is to equip you with the knowledge and skills necessary to effectively utilize the shell method in your mathematical endeavors. Join us as we embark on this enlightening journey through the world of calculus!

What is the Shell Method?

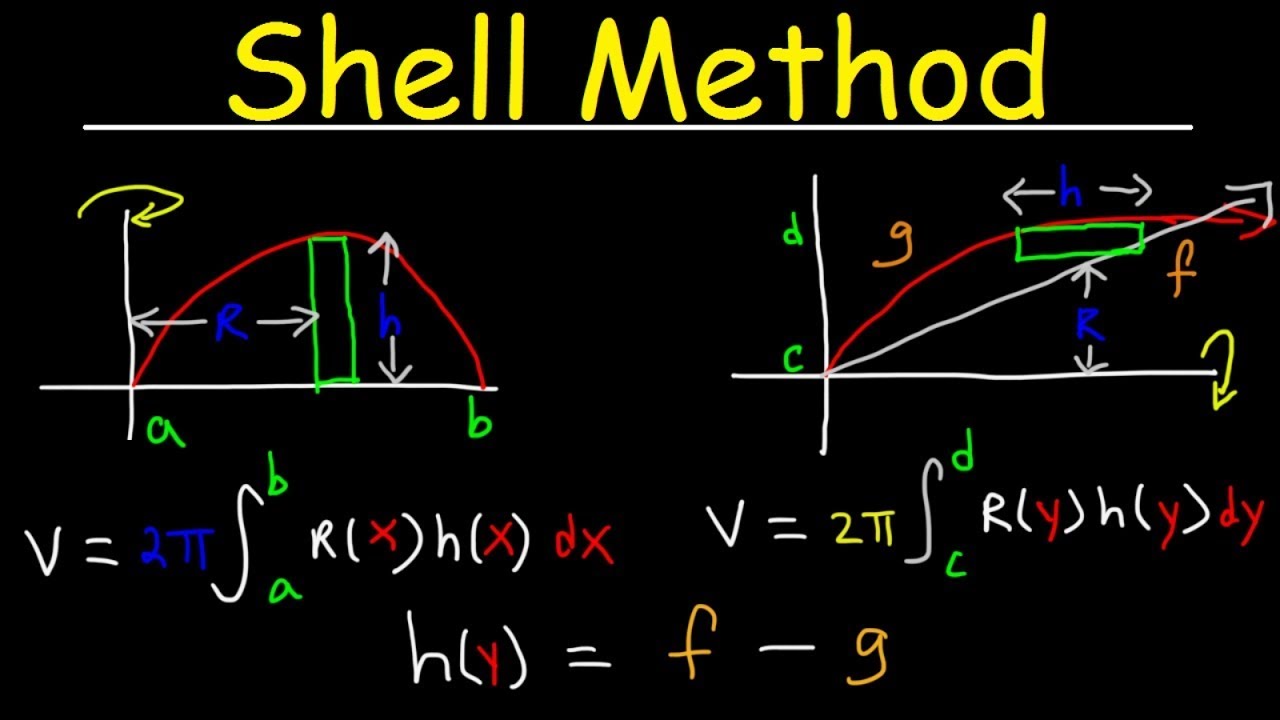
The shell method is a technique used in calculus for finding the volume of a solid of revolution. When you have a region in a plane and you rotate it around an axis, the shape formed is what we refer to as a solid of revolution. The shell method allows you to slice this solid into thin cylindrical shells, which can be summed to find the total volume.

How Does the Shell Method Work?

To understand how the shell method works, consider a region bounded by curves in the first quadrant of the Cartesian plane. When this region is revolved around an axis—let's say the y-axis—it creates cylindrical shells. The volume of each shell can be calculated using the formula:

V = 2πrh, where:
r = radius of the shell (distance from the axis of rotation)
h = height of the shell (length of the function between bounds)

By integrating this formula along the bounds of the region, we can find the total volume of the solid formed by the revolution.

When to Use the Shell Method?

The shell method is particularly effective in situations where the volume of the solid is difficult to compute using other methods, such as the disk or washer method. It's often used when:

The region being revolved is more easily described in terms of height rather than width.
The axis of rotation is vertical, and the function is defined in terms of x.
You need to calculate the volume of a solid that has a complex shape.

What Are the Advantages of Using the Shell Method?

One of the main advantages of the shell method is its versatility. It can be applied to a wide range of problems, including those that would be cumbersome to solve using other techniques. Additionally, the shell method often simplifies calculations when dealing with non-standard shapes or when integrating functions that are difficult to invert.

Can the Shell Method Be Used for Irregular Shapes?

Yes, the shell method can effectively be used for irregular shapes. The key is to accurately define the region and the axis of rotation. By carefully determining the height and radius of the shells, you can still apply the method to calculate the volume of solids that do not conform to regular geometric shapes.

What Are Real-World Applications of the Shell Method?

The shell method has numerous real-world applications across various fields, including:

Engineering: Designing tanks, pipes, and other cylindrical structures.
Physics: Calculating volumes of objects in fluid dynamics.
Architecture: Structural analysis of buildings with rounded shapes.
Manufacturing: Determining material requirements for cylindrical products.

Examples of the Shell Method in Action

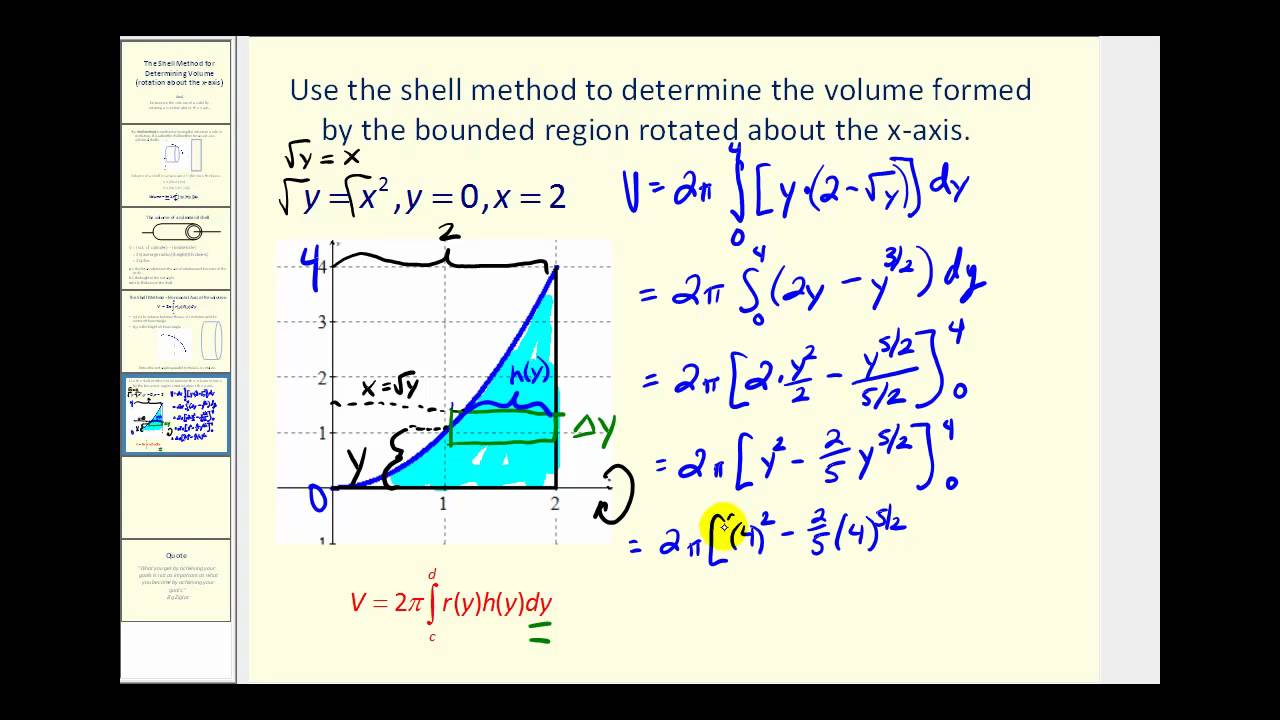
To illustrate the shell method in practice, let’s consider a simple example. Suppose we want to find the volume of the solid formed by revolving the area between the curve y = x² and the x-axis, from x = 0 to x = 2, around the y-axis.

Here’s how we would apply the shell method:

Identify the height: h = x².
Identify the radius: r = x.
Set up the integral for the volume: V = 2π ∫ (from 0 to 2) x(x²) dx.
Compute the integral to find the volume.

What Are Common Mistakes When Using the Shell Method?

While the shell method is a straightforward technique, there are common pitfalls that can lead to errors in calculations:

Incorrectly identifying the axis of rotation.
Confusing height and radius when setting up the integral.
Forgetting to adjust the limits of integration based on the axis of rotation.

How Can One Master the Shell Method?

Mastering the shell method requires practice and a solid understanding of the principles of calculus. Here are some tips to improve your skills:

Work through various examples to build familiarity.
Visualize the solid and the shells to better understand the geometry involved.
Consult additional resources, such as textbooks, online courses, and tutorials.

In conclusion, the shell method is an invaluable tool in the world of calculus, allowing for the computation of volumes with ease and precision. By mastering this technique, you can tackle complex integration problems and apply your skills to real-world scenarios across various fields. Whether you're a student or a professional, understanding the shell method is a key stepping stone in your mathematical journey.