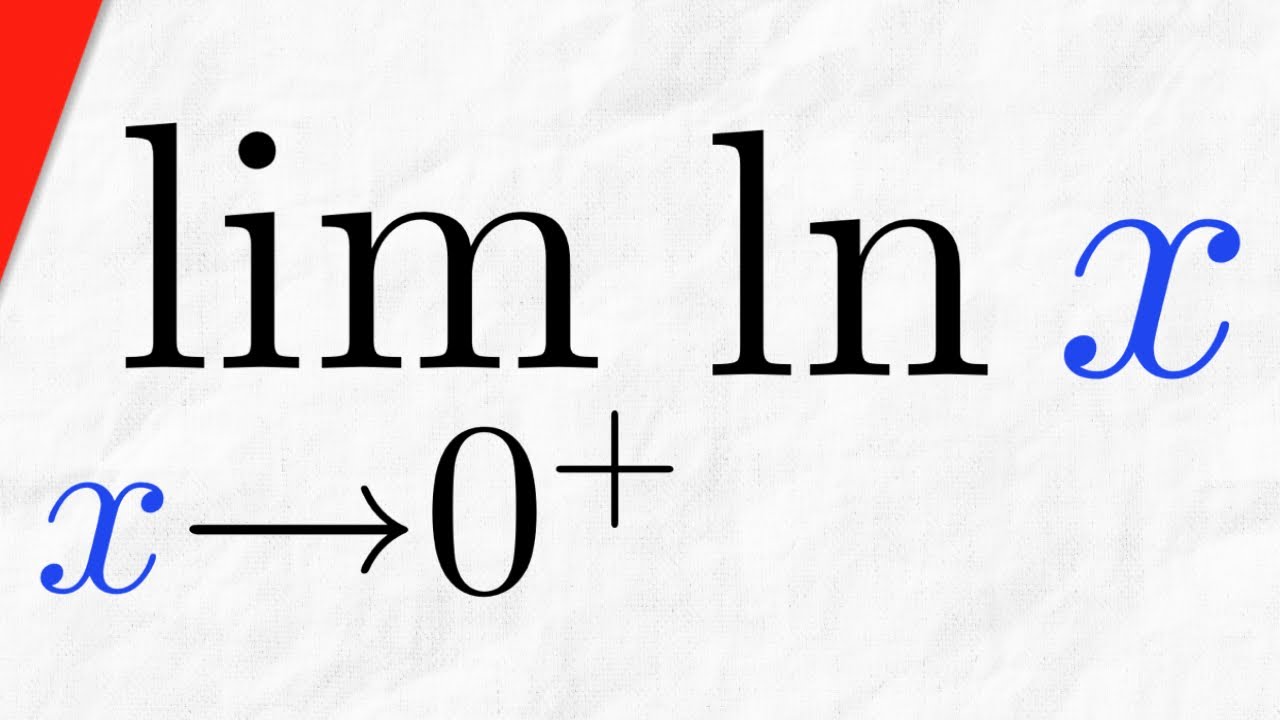When exploring the world of mathematics, particularly calculus and logarithms, one encounters various functions that may seem perplexing at first glance. Among these functions, the natural logarithm, denoted as "ln," plays a significant role in numerous mathematical applications. The question of what happens when we evaluate ln 0 is a common point of confusion and curiosity for many students and enthusiasts alike. This article aims to demystify ln 0, providing clarity on its definition, significance, and the implications of attempting to calculate it. By delving into the intricacies of this mathematical concept, we hope to provide readers with a comprehensive understanding of why ln 0 is deemed undefined.

To understand ln 0, one must first grasp the fundamental properties of logarithms. Logarithms, including the natural logarithm, are the inverse operations of exponentiation. In essence, they answer the question: "To what power must a certain base be raised to obtain a specific number?" For the natural logarithm, the base is Euler's number (approximately 2.71828). As we explore ln 0, we will discuss why it poses a unique challenge and how it contrasts with other logarithmic evaluations.

The topic of ln 0 is not only relevant in theoretical mathematics but also has practical implications in various fields such as engineering, computer science, and economics. Understanding the boundaries and limitations of logarithmic functions can provide deeper insights into exponential growth and decay, which are ubiquitous in real-world scenarios. So, what exactly is ln 0, and why does it spark so much debate among mathematicians?

What is ln 0?

ln 0 refers to the natural logarithm of zero. In mathematical terms, it is represented as ln(0). The function ln(x) is defined only for positive values of x. Therefore, when we attempt to evaluate ln 0, we are attempting to find the logarithm of a non-positive number, which leads us to the conclusion that ln 0 is undefined.

Why is ln 0 Undefined?

To understand why ln 0 is undefined, we must consider the properties of logarithmic functions. The natural logarithm function, ln(x), is defined for all positive real numbers. As x approaches zero from the positive side, the value of ln(x) tends to negative infinity. This means that there is no real number that can satisfy the equation e^y = 0, where y is the natural logarithm. Consequently, this leads to the conclusion that ln 0 does not have a valid output.

What Happens When You Graph ln(x)?

When graphing the natural logarithm function, we observe a continuous curve that approaches negative infinity as x approaches zero from the right. The graph never crosses the y-axis, indicating that there is no defined point for ln 0. This visual representation solidifies the understanding that ln 0 remains undefined within the context of real numbers.

What are the Implications of ln 0 in Mathematics?

The undefined nature of ln 0 has implications in various mathematical disciplines. Here are some key points to consider:

In calculus, the concept of limits is crucial. Evaluating the limit of ln(x) as x approaches zero from the positive side confirms that the limit is negative infinity.
ln 0 highlights the importance of domain restrictions in logarithmic functions, allowing mathematicians to establish boundaries within which functions can be evaluated.
Understanding that ln 0 is undefined aids in problem-solving, particularly in exponential equations where logarithmic identities are employed.

How Does ln 0 Relate to Exponential Functions?

The relationship between logarithmic and exponential functions is foundational in mathematics. The equation y = ln(x) can be rewritten in its exponential form as x = e^y. Given that there is no real number y such that e^y = 0, we reinforce the idea that ln 0 lacks a defined value. This relationship illustrates the interconnectedness of logarithmic and exponential functions, emphasizing the significance of understanding their properties.

Can We Extend the Concept of ln 0 to Complex Numbers?

In the realm of complex numbers, the concept of logarithms can be extended to include values that are not defined in the real number system. However, even in complex analysis, ln 0 remains problematic. While we can use the complex logarithm to evaluate logarithmic values for negative numbers and complex numbers, ln 0 still does not yield a defined value. This highlights the limitations and challenges presented by attempting to define ln 0 in any context.

What Are Common Misconceptions About ln 0?

Several misconceptions surround the concept of ln 0, which can lead to confusion among students and learners:

Some may mistakenly believe that ln 0 could yield a real number, similar to other logarithmic evaluations.
Others may confuse ln 0 with negative logarithmic values, not recognizing that ln 0 is fundamentally different.
There is a tendency to overlook the significance of domain restrictions when working with logarithmic functions.

How Can Understanding ln 0 Benefit Students and Learners?

Grasping the concept of ln 0 and its properties is essential for students as they progress through their mathematical education. Understanding why ln 0 is undefined can enhance their critical thinking skills and encourage them to explore logarithmic functions more deeply. This knowledge can also pave the way for greater comprehension of calculus, complex analysis, and other advanced mathematical concepts.

Conclusion: The Importance of ln 0 in Mathematics

In conclusion, ln 0 serves as a fascinating yet complex topic within the study of logarithmic functions. Its undefined nature underscores the importance of domain restrictions and the intricacies of mathematical functions. By comprehending the implications of ln 0, students and enthusiasts can deepen their understanding of logarithms and their applications across various disciplines. As we continue to explore the world of mathematics, let us embrace the challenges posed by concepts like ln 0 and use them as stepping stones toward greater knowledge and mastery.